Minimum Spanning Tree

A spanning tree is a subgraph that is a tree (a connected undirected graph without cycles) which includes all of the vertices in an undirected graph and all vertices are connected with the minimum number of edges (without any cycles). An undirected graph can have multiple spanning trees.

A minimum spanning tree is a spanning tree with the minimum possible total edge weight in a weighted undirected graph. A weighted undirected graph can have multiple minimum spanning trees.

Two classic algorithms to construct a minimum spanning tree:

• Kruskal's algorithm
• Prim's algorithm

Cut Property

In graph theory, a cut is to put a graph into two disjoint subsets. A crossing edge is an edge that connects a vertex in one subset with a vertex in the other subset.

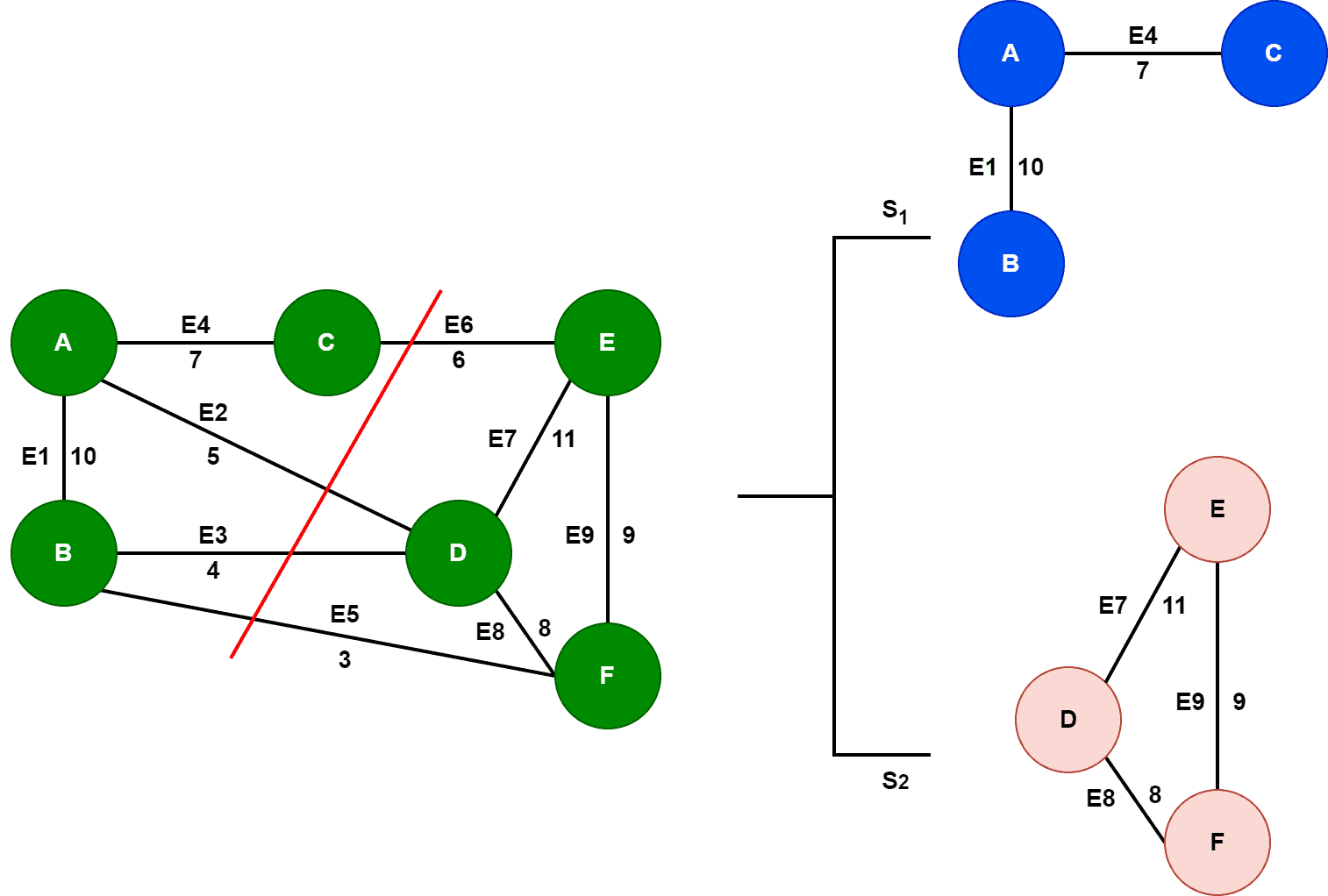
Cut property: for any cut of the graph, the edge with the least weight is also an edge of the minimum spanning tree.

Proof:

• To connect two disjoint subsets, we need to at least one edge.
• If there are more than two edges, it will form a cycle since each disjoin set is connected locally and two added edges will form a cycle.
• If select an edge with a larger weight, that means we can always find a smaller spanning tree by chooses smaller weight. So it has to be the edge with the least weight.