LC611. Valid Triangle Number

Problem Description

LeetCode Problem 611: Given an integer array nums, return the number of triplets chosen from the array that can make triangles if we take them as side lengths of a triangle.

Clarification

• meaning of triplets to make triangles
• contains 0s?

Assumption

• No negative values

Solution

Approach - Sorting + Count

@hiepit provides good explanations

In a triangle, the length of any side is less than the sum of the other two sides, i.e., the following 3 conditions all need to be satisfied:

1. a + b > c
2. a + c > b
3. b + c > a.

If c is the longest side, we just need to check a + b > c since the other two conditions are satisfied. It also excludes a = 0 or b = 0. Since 0 + b > c contradicts the condition c is the longest side.

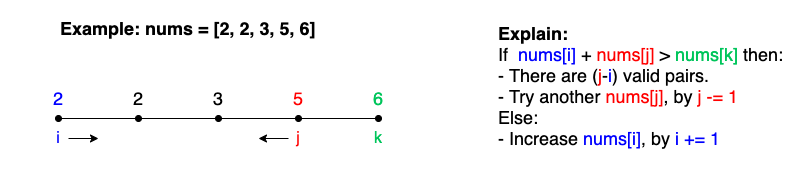
First, sort nums in increase order. Then fix k and select i, j such that i < j < k where nums[i] is the smallest element and nums[k] is the largest element. Start with i = 0 and j = k - 1

• if nums[i] + nums[j] > nums[k]
  • elements in i, i + 1, ..., j - 1 will satisfied this equation and form a triangles. There are total j - i triplets.
  • next step: try another nums[j] by reducing j by 1
• else nums[i] + nums[j] <= nums[k], need to increase sum of nums[i] + nums[j] by increase i by 1

Python

class Solution:
    def triangleNumber(self, nums: List[int]) -> int:
        nums.sort()
        n = len(nums)
        count = 0
        for k in range(2, n):
            i = 0
            j = k - 1
            while i < j:
                if nums[i] + nums[j] > nums[k]:
                    count += j - i
                    j -= 1
                else:
                    i += 1
        return count

Complexity Analysis

• Time complexity: \(O(n^2)\)
  In the worst case, for each k, it goes through 0 ~ k - 1 elements.
• Space complexity: \(O(sorting)\)
  Space used by sorting algorithm

Test

• array contains 0